Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin2 α + cos2 α = 1
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. В заданиях обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.Для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos2 α (для получения тангенса) или на sin2 α (для котангенса).
Рассмотрим задачу Найдите cos α, если известно следующее: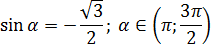
Решение. Нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:sin2 α + cos2 α = 1 3/4 + cos2 α = 1 cos2 α = 1/4 Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Очевидно, это III координатная четверть, где все косинусы отрицательны. cos α = -0,5.
Ответ: -0,5
Проверь себя.
-
Найдите sinα, tg α, ctgα если известно следующее:
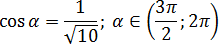
- Найдите cos α, tg α, ctgα если известно следующее:
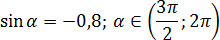
Найдите sinα, tg α, ctgα если известно следующее:
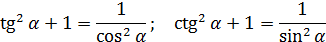
Комментариев нет:
Отправить комментарий